Priority Queues 和 Binary Heap

发表于 | 分类于 |

摘要：

应用

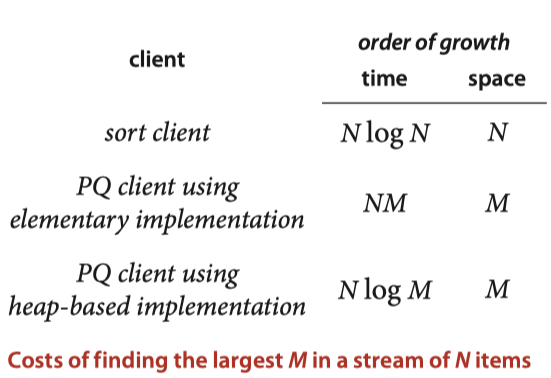
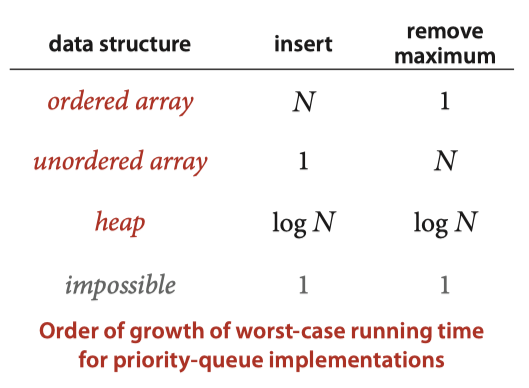
寻找前 M 个最大（小）值

  1. 排序法
  2. PQ Elementary
  3. PQ heap-based

time and space for different methods

追踪序列 median

https://www.youtube.com/watch?v=VmogG01IjYc

https://www.hackerrank.com/challenges/find-the-running-median/problem?h_r=internal-search

https://medium.com/@eranda/running-median-with-heaps-829522330e8a

给定一个整数数组，顺序输入，输出对应每个整数输入后，现有的数组的中位数。

思路：

使用两个 heap，一个大顶堆，所有的值都小于中位数， lowerMaxHeap，一个小顶堆，所有的值都大于中位数 higherMinHeap。这样两个顶堆的顶部就是贡献中位数的数值。这里还存在几个问题

  1. 保证两个顶堆差值不超过1，这样顶部数值才靠近或就是中位数
  2. 中位数计算有两种情况：总数为奇数或偶数。如果为奇数，必然两个顶堆大小查1，那个取出顶堆大小大的那个堆的顶部即为 median。如果为偶数，两个顶堆大小一样，取出两个顶部，求平均值。

注意 Java Priority Queue 的默认是小顶堆，也就是顶部为最小值。另外这里一定别把 大小顶堆和 比中位数大或小混淆。比中位数大的用小顶堆，这样顶部就是比中位数小的数中的较大者，比中位数小的用大顶堆，这样顶部就是比中位数大的数中的较小者。

这个算法完全根据了中位数的特点设计。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
static double[] runningMedian(int[] a) {
	/*
	 * Write your code here.
	 */
	PriorityQueue<Integer> lowerMaxHeap = new PriorityQueue<>();

	PriorityQueue<Integer> higherMinHeap = new PriorityQueue<>(Collections.reverseOrder());

	double[] medians = new double[a.length];

	for (int i = 0; i < a.length; i++) {
		int number = a[i];
		addNumber(number, higherMinHeap, lowerMaxHeap);
		rebalance(higherMinHeap, lowerMaxHeap);
		medians[i] = getMedian(higherMinHeap, lowerMaxHeap);
	}
	return medians;
}

private static double getMedian(PriorityQueue<Integer> lowers, PriorityQueue<Integer> highers) {
	if (lowers.size() == 0 && highers.size() == 0) {
		return 0;
	}
	if (lowers.size() == highers.size()) {
		return (lowers.peek()+highers.peek())/2.0;
	}else if (lowers.size() > highers.size()) {
		return lowers.peek();
	}else {
		return highers.peek();
	}


}

private static void rebalance(PriorityQueue<Integer> lowers, PriorityQueue<Integer> highers) {
	int sizeDiff =  lowers.size() - highers.size() ;
	if (sizeDiff >= 2) {
		highers.add(lowers.poll());
	}else if (sizeDiff <=-2) {
		lowers.add(highers.poll());
	}
}

private static void addNumber(int number, PriorityQueue<Integer> lowers, PriorityQueue<Integer> highers) {
	double median = getMedian(lowers, highers);
	if (number >= median) {
		highers.add(number);
	}else {
		lowers.add(number);
	}

}

Full v.s. Complete Binary Trees

According to wikipedia

  • A full binary tree (sometimes proper binary tree or 2-tree) is a tree in which every node other than the leaves has two children.

?(http://web.cecs.pdx.edu/~sheard/course/Cs163/Doc/FullvsComplete.html)

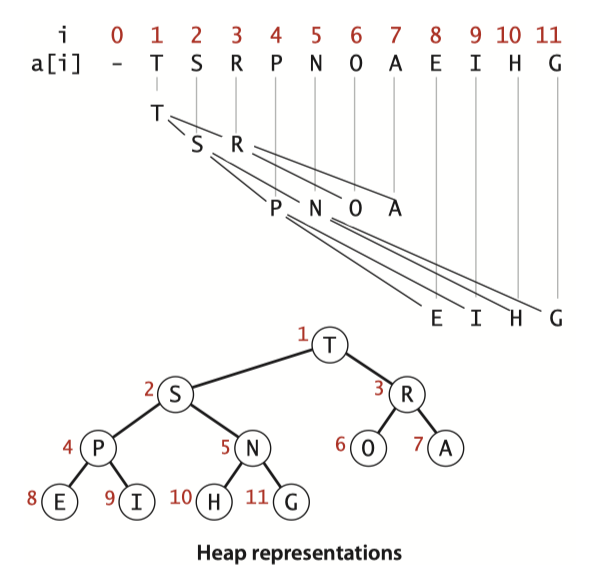
通过观察，二叉完全树是可以压缩为数组表示，不会出现歧义，因为每一层都会尽可能填满，并且填充顺序是从左向右，只有最后一层右侧有空缺。